Python中的浮点数是基于IEEE 754标准的双精度浮点数,占用64位内存,包含1位符号位、11位指数位和52位尾数位,能够表示极大或极小的数值,但在计算过程中常因二进制表示的精度限制产生误差,理解浮点数的计算逻辑和精度处理方法,是准确进行数值计算的关键。
基本运算与精度问题
Python中浮点数的基本运算(加、减、乘、除)直接使用运算符(、、、),但需注意二进制表示导致的精度误差,十进制中的0.1无法精确转换为二进制,存储时会截断为近似值,导致1 + 0.2的结果不等于3,而是30000000000000004,这种误差源于浮点数的存储机制:计算机用二进制科学计数法表示小数时,部分十进制小数会转换为无限循环二进制小数,而52位尾数无法完整存储,只能截断取近似值。
精度处理方法
内置函数round()
round()函数用于对浮点数进行四舍五入,语法为round(number, ndigits),其中ndigits指定保留的小数位数。round(0.1 + 0.2, 2)结果为3,但需注意round()采用“银行家舍入法”(即对5舍入时,若前一位为偶数则舍,奇数则入),可能导致非预期结果,如round(2.5)结果为2,round(3.5)结果为4。
decimal模块
对于高精度计算(如金融场景),可使用decimal模块,它提供十进制浮点数运算,避免二进制误差,使用时需先导入模块,并通过getcontext().prec设置精度位数。
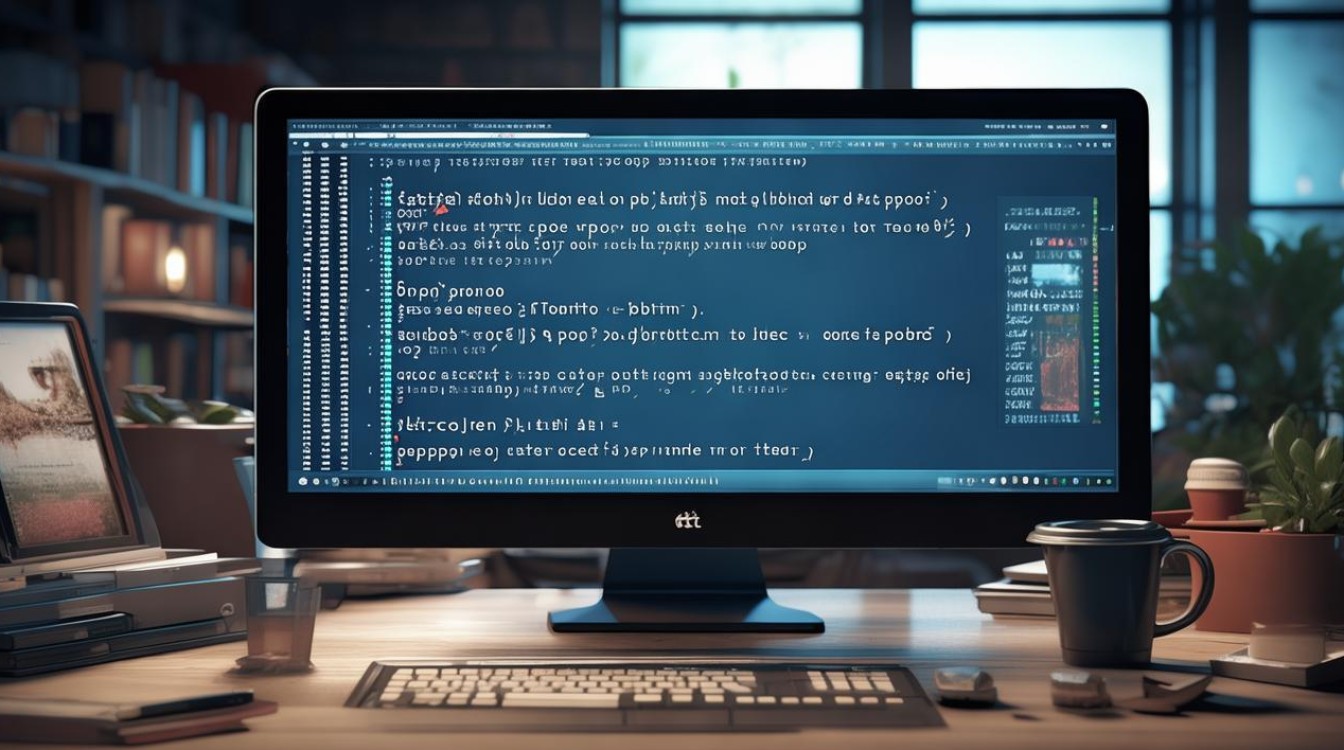
from decimal import Decimal, getcontext
getcontext().prec = 6 # 设置精度为6位
result = Decimal('0.1') + Decimal('0.2') # 结果为Decimal('0.3')
decimal模块支持字符串形式的初始化(避免直接使用浮点数引入误差),并提供精确的舍入控制(如ROUND_HALF_UP)。
比较浮点数
直接使用比较浮点数可能因误差导致误判,建议使用math.isclose()函数,通过设置相对误差和绝对误差阈值判断两个浮点数是否“接近”。
import math math.isclose(0.1 + 0.2, 0.3, rel_tol=1e-9, abs_tol=1e-9) # 返回True
浮点数精度问题对比
| 现象 | 原因 | 解决方法 |
|---|---|---|
| 1 + 0.2 ≠ 0.3 | 二进制截断误差 | 使用decimal模块 |
| round(2.5) = 2 | 银行家舍入法 | 明确舍入模式 |
| 直接比较浮点数误差 | 存储精度差异 | 使用math.isclose() |
相关问答FAQs
Q1:为什么Python中1 + 0.3的结果是4000000000000001而不是4?
A:这是因为0.1和0.3在二进制中都是无限循环小数(0.1的二进制为0.0001100110011...,0.3为0.0100110011001...),计算机用52位尾数存储时会截断,导致相加后产生微小的正误差,可通过decimal模块或格式化输出(如f"{0.1 + 0.3:.10f}")控制显示精度。

Q2:decimal模块和round()函数在处理浮点数精度时有何区别?
A:round()是对浮点数的近似值进行四舍五入,本质仍是二进制运算后的结果,无法消除原始存储误差,适用于显示场景;而decimal模块基于十进制运算,通过字符串初始化避免二进制误差,支持自定义精度和舍入模式,适用于需要精确计算的场景(如货币计算)。




